JinWoo Kim

백문이 불여일견, 백견이 불여일행.

8 minute read

통계 - 개념 정리

단순 회귀분석

회귀분석

  • 변수들간의 함수적 관계를 선형으로 추론하는 통계적 분석 방법
    • 독립변수를 통해 종속변수를 예측하는 방법
  • 비선형인 함수적 관계일 경우 비선형회귀를 사용

종속 변수

  • 다른 변수의 영향을 받는 변수
  • 반응변수라 표현하기도 함.
  • 예측을 하고자 하는 변수

독립 변수

  • 종속변수에 영향을 주는 변수
  • 설명변수라 표현하기도 함.
  • 예측하는 값을 설명해주는 변수

단순 회귀 분석

  • 하나의 독립변수로 종속변수를 예측하는 회귀모형을 만드는 방법

다중 회귀 분석

  • 2개 이상의 독립변수로 종속변수를 예측하는 회귀모형을 만드는 방법

회귀 모델링 분류

  • Regression Models

    • Simple(단순)

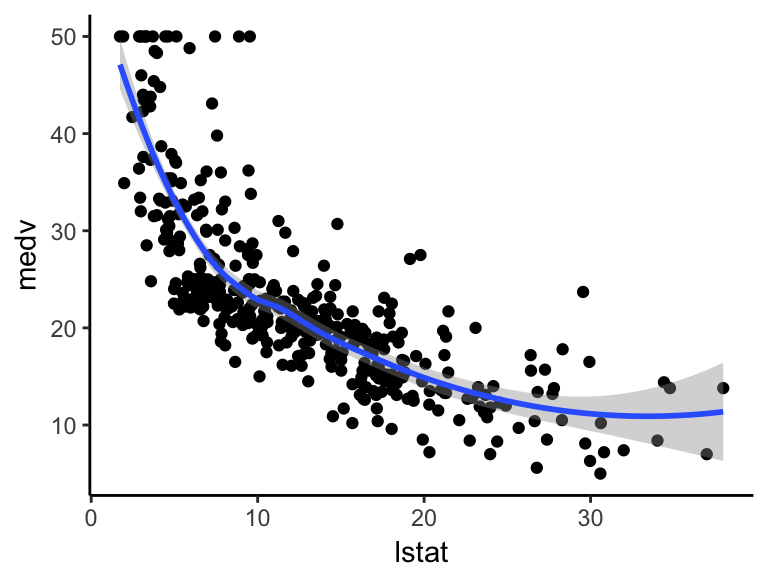
      • Linear(선형)

      • Non-linear(비선형)

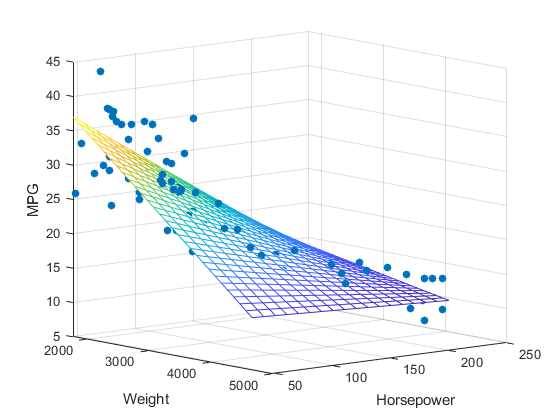
    • Multiple(다중)

      • Linear(선형)

      • Non-linear(비선형)

단순 회귀분석

  • 회귀선을 $y = \beta_0 + \beta_1X + \epsilon$

  • 회귀선으로부터 각 관측치의 오차를 최소로 하는 선을 찾는것이 핵심.

  • 오차를 최소로 하여 $\beta_0,\beta_1$을 추정하는 방법을 최소제곱법(method of least squares)이라 한다.

최소제곱법

  • 회귀모형의 모수 $\beta_0,\beta_1$을 추정하는 방법중 하나.

  • 회귀모형의 모수를 회귀계수라고 한다.

  • 최소제곱법을 통해 구한 추정량을 최소제곱추정량(LSE)

  • 최소제곱법을 통해 회귀모형의 모수를 추정하는것을 OLS(Ordinary Least Square)라고 함.

  • 회귀 모형의 오차에 대하여 기본 가정이 있음

    1. 정규성 가정
      • 오차항은 평균이 0인 정규 분포를 따름
    2. 등분산성 가정
      • 오차항의 분산은 모든 관측값 $x_i$에 상관없이 일정함
    3. 독립성 가정
      • 모든 오차항은 서로 독립임
  • 오차항의 제곱합

    • $SS = \Sigma{\epsilon_i^2} = \Sigma{(y_i - \beta_0-\beta_1x_i)^2} = \frac{S_{xy}}{S_{xx}}$

    • 단,
      $S_{xx} = \Sigma{(x_i-\overline{x})^2}$,
      $S_{xy} = \Sigma{(x_i-\overline{x})(y_i-\overline{y})}$

분산분석표

  • 추정된 회귀식에 대한 유의성 여부는 분산분석을 통해서 회귀식의 유의성을 판단 할 수 있음

  • $y_k - \overline{y} = (y_k-\hat{y_k}) + (\hat{y_k} - \overline{y_k})$

  • SST(총제곱합) = SSE(잔차제곱합) + SSR(회귀제곱합)

    • 자유도 n-1 = (n-2) + 1

  • 제곱합을 각각의 자유도로 나눈값을 평균제곱(mean square)이라고 함.

  • 평균제곱오차(mean square error) = $\hat{\sigma^2}$

  • 회귀평균제곱(regression mean square) = SSR / 1

회귀분석의 추론과 가설검정

결정 계수

  • Coefficient of determination : $R^2$

  • 추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값

  • $R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST}$

  • 0과 1 사이의 값으로, 1에 가까울수록 추정된 모형이 설명력이 높다.

  • 0일때 추정된 모형이 설명력이 전혀 없다고 할수 있음.

수정 결정 계수

  • $R^2$은 유의하지 않은 변수가 추가되어도 항상 증가됨(다중회귀시 발생)

  • Adjust $R^2$은 특정 계수를 곱해줌으로서 $R^2$가 항상 증가하지 않도록 함

  • 보통 모형간의 성능을 비교할때 사용함

  • $R_{adj}^2 = 1-[\frac{n-1}{n-(p+1)}]\frac{SSE}{SST}$

    • p는 변수의 개수

잔차 분석

  • 선형성을 벗어나는 경우
    • 종속변수와 독립변수가 선형 관계가 아님
  • 등분산성이 벗어난 경우
    • 일반적인 회귀모형 사용 불가능
    • 등분산성 가정 위배
  • 독립성에 벗어나는 경우
    • 시계열 데이터 또는 관측 순서에 영향을 받는 데이터에서는 독립성을 담보할 수 없음
      • Durbin-Watson test 실행
  • 정규성을 벗어나는 경우
    • Normal Q-Q plot으로도 확인
    • 잔차가 -2 ~ +2사이에 분포해야함
    • 벗어나는 자료가 많으면 독립성 가정 위배

다중 회귀 분석

다중 회귀 분석

  • 2개 이상의 독립변수로 종속변수를 예측하는 회귀모형을 만드는 방법

    • $Y=\beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_iX_i + \epsilon_i$
  • 로지스틱 회귀 분석
    • 반응 변수가 범주형(이진수)인 경우 사용하는 모형
  • 다항 회귀분석

    • 독립변수가 k개이고 반응변수와 독립변수가 1차함수 이상인 회귀 분석

    • 파생 변수 : 기존에 있는 변수의 조합으로 새로운 변수를 만드는것.

    • 파생변수를 활용해서 다항으로 회귀분석해야하는 경우가 종종 있다고 한다.

변수선택법

  • 전진 선택법
    • 독립변수를 1개부터 시작하여 가장 유의미한 변수들부터 하나씩 추가하면서 모형의 유의성을 판단하는 방법
  • 후진 제거법
    • 모든 독립변수를 넣고 모형을 생성한 후, 하나씩 제거하면서 판단하는 방법
  • 단계적 방법
    • 위의 두가지 방법을 모두 사용하여 변수를 넣고 빼면서 판단하는 방법

번외) AIC

  • Akaike Information Criterion
  • 통계 모델간의 적합성을 비교할수 있는 수치
  • 적을수록 모형의 성능이 좋아짐.
  • 보통 프로그램을 통해 구한다.
  • AIC = 2(log-likelihood) + 2k

    • k : 모형 파라미터의 개수(모형에서 상수항을 포함한 설명변수의 갯수)

    • log-likelihood : 모형 적합도를 나타내는 척도

  • 정규분포를 따르는 잔차를 가진 경우의 최소제곱을 이용한 회귀분석에는 아래의 공식을 대신 사용할수 있다.

    • $ AIC = n log(\hat{\sigma}^2)+2k$

    • $\hat{\sigma}^2$ : $\frac{SSR}{n}$

    • n : 표본의 크기
    • k : 모형 파라미터의 개수

더미 변수

  • 값이 0 또는 1로 이루어진 변수

  • 범주형 변수를 사용하기 위해 범주에 임의로 생성하는 변수

  • 예시

    • 최종학력 : 고졸, 대졸,석사, 박사 4가지를 표현해야 할때

      • 범주형 변수를 0과 1의 조합으로 표현할수 있도록 더미변수를 4-1개 생성.

다중공선성

  • 상관관계가 높은 독립변수들이 동시에 사용될때 문제가 발생

  • 결정계수 $R^2$값은 높아 회귀식의 설명력은 높지만, 독립변수의 P-value 커서 개별인자들이 유의하지 않는 경우 의심할수 있음.

  • 일반적으로 분상팽창요인(Variance Inflation Factor, VIF)이 10이상이면 다중공선성이 존재함
    • $VIF = \frac{1}{1-R_{k}^2}$
      • $R_k^2$ :k번째 독립변수를 종속변수로, 나머지를 독립변수로 하는 회귀모형의 결정계수

  • 다중공선성이 문제가 되는 이유

    • 예측에서 신뢰구간을 결정하는 요인 = 분산
    • 다중공선성이 발생한다는것은 분산이 커진다는 의미.
    • 즉, 신뢰구간이 의미가 사라짐.

  • 해결 방안

    1. 다중공선성이 존재하지만 유의한 변수인경우 목적에 따라서 사용할수 있음

    2. 변수 제거

    3. 주성분분석으로 변수를 재조합

분산 분석

  • 셋 이상의 모집단으로부터 추출한 양적 데이터를 비교하는 통계적 분석 방법

분산 분석

  • analysis of variance, ANOVA

  • 셋 이상의 모집단의 평균 차이를 검정

  • 세개의 모집단을 t-test로 검정한다면

    • 세번 검증해야 한다(모집단1-2,1-3,2-3).
    • 오차가 커진다(a=0.05일때, 3번의 비교로 $a=1-(1-0.05)^3 = 0.143$)

실험계획법

  • 모집단의 특성에 대하여 추론하기 위해 특별한 목적성을 가지고 데이터를 수집하기 위한 실험설계를 실험계획법이라고 함

  • 반응변수 : 관심의 대상이 되는 변수

  • 요인/인자(Factor) : 실험환경 또는 조건을 구분하는 변수로 실험에 영향을 주는 변수

  • 인자수준 : 인자가 취하는 개별 값(처리 : treatment)

분산분석을 사용하는 이유

  • 모집단의 평균들을 비교하기 위하여 특성값의 분산 또는 변동을 분석하는 방법

  • 실험을 통해 얻은 편차의 제곱합을 통해 평균의 차이를 검정

분산분석의 기본 가정

  1. 각 모집단은 정규분포를 따른다
  2. 각 모집단은 동일한 분산을 갖는다
  3. 각 표본은 독립적으로 추출되었다.

분산분석의 가설과 실험의 가정

가설

  • $H_0 : $ 각 집단의 평균은 동일하다 vs $H_1 : $ 각 집단의 평균에 차이가 있다.

실험의 가정

  • 반복의 원리
    • 실험을 반복해서 실행해야 함
  • 랜덤화의 원리
    • 각 실험의 순서를 무작위로 해야함
  • 블록화의 원리
    • 제어해야할 변수가 있다면 인자에 영향을 받지 않도록 조건을 묶어서 실험해야 함

분산분석의 종류

  • 일원 분산분석
    • 한가지 요인을 기준으로 집단간의 차이를 조사하는 것
  • 이원 분산분석
    • 두가지 요인을 기준으로 집단간의 차이를 조사하는 것
  • 다원 분산분석
    • 세가지 이상의 요인을 기준으로 집단간의 차이를 조사하는 것

일원 분산분석

  • One-way ANOVA

  • 한개의 반응변수, 한개의 독립 인자

  • 반응 변수 : 연속형 변수만 가능

  • 독립 인자(변수) : 이산형 또는 범주형 변수만 가능

  • 분산분석표

  • 가설 : 적어도 하나 이상의 평균이 같지 않다

    • 검정통계량
      • $F = \frac{MS_{tr}}{MSE}$, 귀무가설하에서 F의 관측값 : $f_0$
    • 기각역(유의수준 $a$)
      • $f_0 \ge F_a(k-1,N-k)$이면 $H_0$를 기각
    • 유의확률(p값)
      • $F \sim F(k-1,N-k)$일때, $p$값 = $P{F \ge f_0}$이고 $p$값이 $a$보다 작으면 $H_0$를 기각

사후 검정

  • 평균이 다른건 알지만, 어떤 처리 조건이 평균 차이가 있는가?

  • Bonferroni, scheffe, Duncan, Dunnett등의 방법으로 사후 검정이 가능

이원 분산분석

  • two-way ANOVA

  • 한개의 반응변수와 두개의 독립인자로 분석하는 방법

  • 독립인자는 one-way와 마찬가지로 이산형 또는 범주형 변수만 가능

상호작용

  • 한 독립변수의 main effect가 다른 독립변수의 level에 따라서 원래의 선형관계를 비선형관계로 변하게 만드는 경우

가설

  • 상호작용으로 인해, 총 세가지 가설을 세워야 한다.

  • 첫번째 main effect 가설
    • 첫번째 독립변수에 대해 적어도 하나 이상의 평균이 같지 않다.
  • 두번째 main effect 가설
    • 두번째 독립변수에 대해 적어도 하나 이상의 평균이 같지 않다
  • 상호작용에 대한 가설
    • $H_0$ : 상호작용이 없다 vs $H_1$ : 상호작용이 있다

시계열

  • 시간의 흐름에 따라서 관측된 자료를 통계적으로 분석하는 방법

시계열 분석

  • 시계열 데이터를 분석하고 여러 변수들간의 인과관계를 분석하는 방법

  • 시계열 데이터
    • 시간을 기준으로 관측된 데이터
    • 일,주,월,분기,년 또는 Hour등의 시간 경과에 따라 관측한 데이터.
    • 시계열 데이터는 연속 시계열과 이산 시계열 데이터로 구분할수 있음.
  • 연속 시계열
    • 자료가 연속적으로 생성
    • 대부분의 데이터 형태가 연속형이나 이산형 정의하여 분석
  • 이산형 시계열
    • 일정시차(간격)을 두고 관측되는 형태의 데이터
    • 대부분 이산형 데이터를 분석

시계열 분석의 목적

  • 예측
    • 미래의 특정 시점에 대한 관심의 대상(반응변수)을 예측
  • 시계열 특성 파악
    • 경향, 주기, 계절성, 변동성 등 관측치의 시계열 특성 파악

전통적인 시계열 분석 방법

  • 이동 평균 모형(MA, moving average)
    • 최근 데이터의 평균을 예측치로 사용
  • 자기 상관 모형(AR, Autocorrelation)
    • 변수의 과거 값의 선형 조합을 이용하여 예측하는 방법
  • ARIMA
    • Autoregressive Integrated Moving Average
    • 관측값과 오차를 사용해서 모형을 만들어 미래를 예측
    • 이동평균모형 + 자기상관모형
  • 지수평활법
    • 현재에 가까운 시점에 가장 많은 가중치를 주고, 멀어질수록 낮은 가중치를 주어서 미래를 예측하는 방법

시계열 요소

  • 경향/추세
    • 시계열 데이터가 장기적으로 증가(감소)할때, 추세가 존재한다.
  • 계절성
    • 특정 기간마다 어떤 특정시기에 나타나는것같은 요인을 계절성요인이라 함.
    • 계절성 요인이 시계열에 영향을 줄때 계절성이라고 한다.
  • 주기성
    • 일정한 주기(진폭)마다 유사한 변동이 반복되는 현상.
  • 불규칙 요인
    • 예측하거나 제어할수 없는 요소
      • ex)회귀분석의 오차와 같은 항목

시계열 분석 방법

  • 단기 예측
    • 방법론
      • 지수평활법
      • 시계열 해법
      • Box-jenkins 방법
    • 데이터 및 예측
      • 수학적 이론에 의존
      • 시간에 따른 변동이 많은(빠른) 시계열 자료에 적용
  • 장기 예측
    • 방법론
      • 회귀분석 방법론
    • 데이터 및 예측
      • 장기적으로 예측이 필요한 데이터
  • 직관적 방법
    • 방법론
      • 지수평활법
      • 시계열 분해
    • 데이터 및 예측
      • 시간에 따른 변동이 느린 데이터에 활용
  • 다중 시계열
    • 방법론
      • 회귀분석(계량경제) 방법
      • 전이함수모형
      • 다변량 ARIMA
    • 데이터 및 예측
      • 시계열데이터와 설명변수가 있는 경우

이동평균법

  • 단순이동평균
    • $\overline{Y_{t,m}} = \frac{y_t+y_{t-1}+\cdots+y_{t-m+1}}{m}$

지수평활법

  • 모든 관측값을 이용하면서 예측하는 시점에 가까울수록 비중을 두어 최근값이 예측시 더 많은 기여를 하도록 만드는 방법

  • $F_{t+1} = wF_t + (1-w)F_{t-1},\quad t \ge 2$
    • w는 지수평활계수
  • 지수평활계수
    • 0~1사이의 계수.
    • 1에 가까울수록 최근 관측값에 더 많은 비중을 주는것을 의미함.

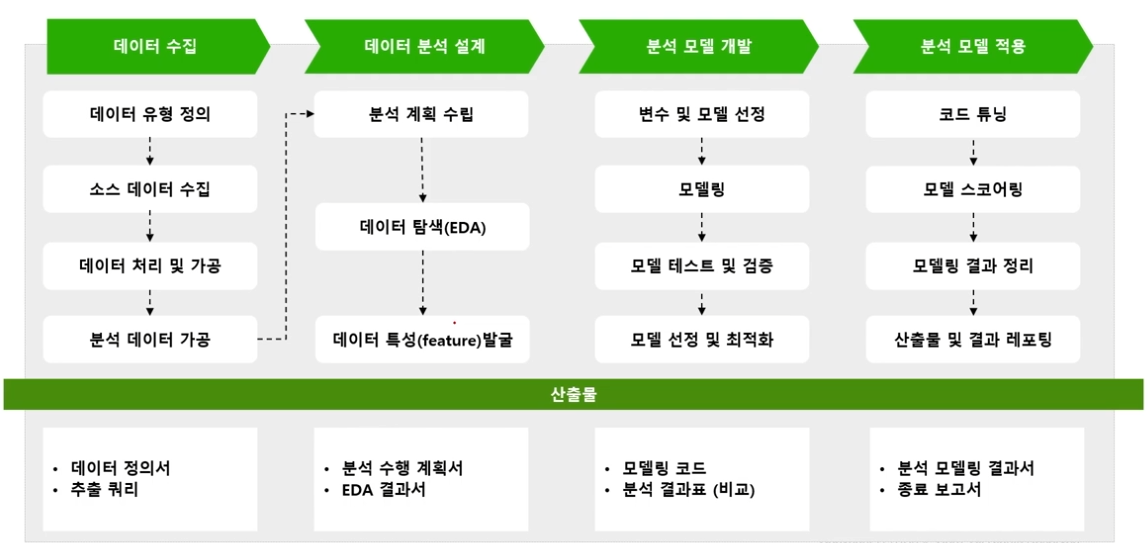
데이터 분석 프로세스

머신러닝

  • 인공지능의 한 분야

  • 컴퓨터가 학습할수 있도록 하는 알고리즘과 기술을 개발하는 분야

  • 컴퓨터가 학습모형을 기반으로 주어진 데이터를 통해 스스로 학습하는 것.

  • 인공지능 $\supset$ 머신러닝 $\supset$ 딥러닝

  • 머신러닝의 3요소(T. Michell, 1997)
    • Task
    • Experience
    • Performance
  • Task를 달성하기 위해 경험을 통해 성능을 개선시킨다.
    • 분석하고자 하는 목표(T)를 정의
    • Experience를 정의하기 위한 데이터를 수집
    • Performance를 향상시키기 위한 Measure를 정의

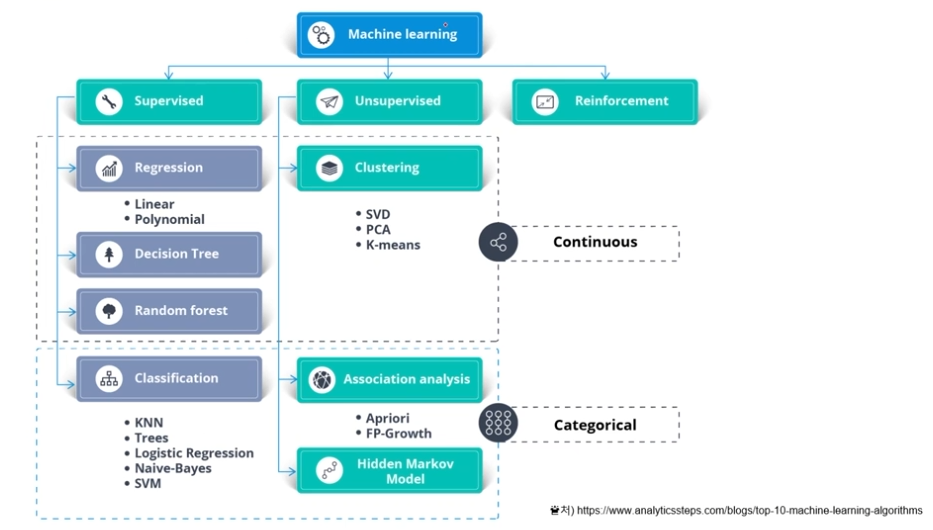
지도학습

  • Supervised Learning
  • Label이 있는 데이터에 대해서 분석하는 방법.
  • 과거의 데이터로 미래를 예측하는 방법
  • Classification
    • Y값이 Category일때 사용
  • Regression
    • Y값이 연속된 값일때 사용

비지도학습

  • Unsupervised Learning
  • Label이 없는 데이터에 대해 분석하는 방법
  • 데이터를 나누거나(군집화), 속성별로 분류할때 사용

강화학습

  • Reinforcement Learning
  • 행동과 정책에 따른 보상을 통해 원하는 행동을 강화하는 방식.

기계학습 알고리즘 종류

Decision Tree

  • 설명변수(X)간의 관계나 척도에 따라 목표변수(Y)를 예측하거나 분류하는 문제에 활용되는 나무 구조의 모델

  • 장점
    • 결과 해석이 쉽고 빠름
    • 선형/비선형에 적용 가능
  • 단점
    • 과도적합의 문제 조심
    • 분기점에서 오차 발생확률이 올라감

앙상블 모형

  • Bagging
    • bootstrap aggregating
    • 데이터를 여러번 복원추출하는 방식으로 여러 표본을 만들어 이를 기반으로 각각의 모델을 개발한 후 결과를 하나로 합쳐 하나의 모델을 만들어 내는것
    • ex) Random Forest(Decision Tree를 여러번 복원추출하는 방식)
      • Decision Tree의 단점인 과도적합 문제를 어느정도 해소 가능
  • Boosting

    • Bagging과 동일하게 복원 랜덤 샘플링을 하지만, 가중치를 부여한다

    • Bagging은 병렬로 학습하지만, Boosting은 순차적으로 학습시킨다.

    • 학습이 끝나면 나온 결과에 따라 가중치가 재분배된다.

    • ex) AdaBoost, XGBoost, GradientBoost

추천 모형

  • Collaborative Filtering(CF 모형)

    • 사용자 기반 협업 필터링

      • 비슷한 행동을 한 사용자를 클러스터링하여 목표사용자가 속하는 군집에서 다른 사람들이 높은 점수의 평가를 부여한 아이템을 추천

    • 아이템 기반 협업 필터링

      • 아이템 사이의 연관성을 파악하여 비슷한 아이템의 군집을 생성하고, 그 군집 내에서 목표 사용자의 행동 기록을 기반으로 다른 아이템을 추천

Deep Learning

  • Deep Neural Network라고도 불림.

  • 인공신경망의 발전한 형태

  • 인간의 뇌처럼 수많은 노드를 연결, 노드값을 훈련시켜 데이터를 학습시킴.

  • CNN
    • Convolutional Neural Network
    • 데이터 -> 특징 -> 지식의 단계로 학습
    • ex) 사물인식에 있어서 특징점인 선이나 색을 먼저 추출하여 판단
  • RNN
    • Recurrent Neural Network
    • 시계열 데이터 분석에 사용함
    • 매 순간마다 인공신경망 가중치를 쌓아올리는 형태

강의 외 참고 자료

You May Also Enjoy